统计学中数据挖掘和机器学习中的决策树训练,使用决策树作为预测模型,一般的,一棵决策树包含一个根结点、若干个内部结点和若干个叶结点。叶结点对应于决策边界,其他每个结点则对应于一个属性测试(或特征测试);每个结点包含的样本集合根据属性测试的结果被划分到子结点中;根结点包含样本全集。决策树学习的目的是为了产生一棵泛化能力强,即处理其他未知示例能力强的决策树。
一棵树训练过程:根据一个指标,分裂训练集为多个子集,这个过程不断的在产生的子集里重复递归进行,即递归分割。当一个训练子集的类标都相同时停止递归。这种决策树的自顶向下归纳是贪心算法的一种,也是目前最为常见的一种训练方法。
决策树类型
在机器学习中,决策树主要有两种类型
- 分类树 :输出样本的类标
- 回归树 :输出实数值
分类和回归树,简称CART(Classfication and Regression Tree)包含上述两种决策树。
集成学习生成多棵树:
- 装袋算法(Bagging):早期集成方法,用有放回的抽样法来训练多棵决策树,最终结果用投票法产生。
- 随机森林(Random Froest):使用多棵决策树来改进分类功能。
- 提升树(Boosting Tree):可以用来做回归分析和分类决策
- 旋转森林(Rotation Forest):每棵树的训练首先使用主成分分析法(PCA)
决策树划分
1.信息增益
信息熵(information entropy):度量样本集合纯度的常用指标
假设样本集合为D,其中的某一k类样本所占比例为$p_k$(k=1,2,…,|y|),则D的信息熵定义如下:
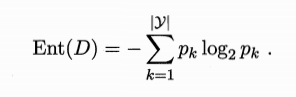
Ent(D)的值越小,则D的纯度越高
Ent(D)的最小值为0,最大值为$\log _2\left | y \right |$
信息增益(information gain):
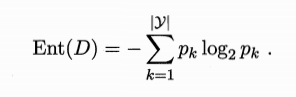
一般而言,信息增益越大,意味着通过该属性进行划分所获得的“纯度提升”越大。因此,可以通过信息增益最大的来作为选择划分属性。
这其中ID3(ID, Iterative Dichotomiser 迭代二分器)决策树学习算法就是以信息增益为准则来选择划分属性的。
2.增益率
为减少信息增益准则对可取数值数目较多的属性有所偏好而带来的不利影响,C4.5决策树算法改为使用增益率(gain ratio)来选择最优划分属性。
增益率定义为:
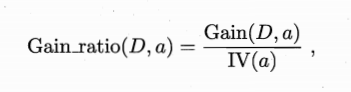
其中
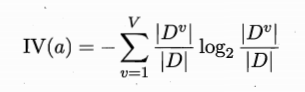
称为属性a的“固有值”。并且属性a的可能取值数目越多(即V越大),则IV(a)的值也会越大。
增益率准则对可取值数目较少的属性有所偏好。
3.基尼指数
数据集D的纯度可用基尼值来度量:

Gini(D)表示:从数据集D中随机抽取两样本,其类别标记不一致的概率。因此,Gini(D)越小,则数据集D的纯度越高。
如果使用属性a来定义基尼指数
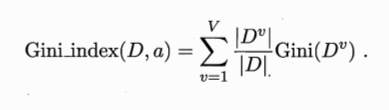
因此,在候选属性集合A中,选择基尼指数最小的属性作为最优划分属性。
决策树剪枝
剪枝处理是决策树学习算法解决过拟合的一个重要手段。
基本策略
预剪枝
在决策树生成过程中,对每个结点在划分前先进性估计,若当前结点的划分不能带来决策树泛化性能的提升,则停止划分并将当前结点标记为叶结点。
后剪枝
先从训练集中生成一棵完整的决策树,然后自底向上的对非叶结点进行考察估量,若将该结点对应的子树替换为叶结点能带来决策树泛化能力的提升,则将该子树替换为叶结点。
决策树连续与缺失值
连续值处理:采用二分法对连续属性进行处理(C4.5算法)
缺失值处理:插值法(Imputation)、替代法(Alernate/Surrogate Splits)、缺失值单独分支(Missing value brance)、概率权重(Probability weights)
决策树优缺点
优点
- 易于理解和解释 人类善于这种决策思维。
- 只需很少的数据准备 几乎不需要数据归一化处理。
- 可以处理数值型数据也可以处理类别型数据 一般其他技术都只可以处理一种数据类型。
- 使用白箱模型 输出结果容易通过模型的结构来解释。而神经网络是黑箱模型,很难解释输出结果。
- 可以通过测试集来验证模型的性能 整体模型稳定
- 强健控制 对噪声处理有好的鲁棒性
- 可以很好的处理大规模数据
缺点
- 训练一棵最优的决策树是一个完全NP问题。因此实际应用时,决策树的训练采用启发式搜索算法(比如:贪心算法)来达到局部最优。这样是无法得到最优决策树的。
- 决策树创建的过度复杂会导致无法很好的预测训练集之外的数据。这就是过拟合问题,使用剪枝机制可以避免这种问题。
- 有些问题决策树没办法很好的解决,比如异或问题。处理这种问题决策树会变得过大。因此如果要处理,只能通过改变问题的领域或者使用其他更为耗时的学习算法(例如:同级关系学习 OR 归纳逻辑编程)
- 对类别型属性的数据,信息增益会有一定偏好