文章
138
标签
73
分类
8
首页
重拾Android
LeetCode
AI头条
论文推荐
分类
标签
归档
友链
关于
充电驿站
目录
  1. 1. 比赛流程
    1. 1.1. 背景介绍
    2. 1.2. 数据集
    3. 1.3. 导库 & 加载
    4. 1.4. Data Dictionary
    5. 1.5. Exploratory Data Analysis
      1. 1.5.1. 1、处理数据
      2. 1.5.2. 2、特征工程
      3. 1.5.3. 3、缺失数据处理（清理数据）
      4. 1.5.4. 4、建模
  2. 2. 总结
【竞赛专题】Kaggle Titanic入门
|机器学习
字数总计: 3.8k|阅读时长: 15 分钟|阅读量:

Kaggle——作为一款以举办机器学习竞赛、编写和分享代码的平台，正在被越来越多的数据分析爱好者所青睐，这其中更是吸引了数以十万计数据科学家的关注。也正于此，才会被谷歌收入麾下。本人作为一名萌新，本着对机器学习的执著与热爱，在参考多篇文章之后，希望可以为同样喜爱Kaggle的盆友记录写下一点东西，再次感谢那些引路者，正是因为你们，国家在AI这条路上才能越走越远，才会越发强盛。

比赛流程

  • 1、赛题背景了解（这会影响第四步）
  • 2、数据集下载
  • 3、分析数据
  • 4、数据处理与特征工程
  • 5、模型评估与选择
  • 6、结果预测提交
  • 7、算法模型优化

上述步骤，以Kaggle竞赛题《Titanic: Machine Learning from Disaster》为样例，预测泰坦尼克号乘客幸存来熟悉机器学习基础知识以及竞赛流程。具体每个步骤所涉及的操作官网均有介绍，相信也更有说服力，这里直接贴代码分析。

背景介绍

耳熟能详的『Jack and Rose』爱情故事延传至今，船长的一句『Lady and kid first！』给原本悲怆黯然的故事增添了敬意，或许这对在当时惊恐万分的人们来说是末日，但时至今日，借助机器之力生成预测模型，是否可以做些预测，让更多的人存活下去，我们可以试试。

数据集

  • gender-submission.csv 待提交样例：该预测集只是假设女性乘客幸存下来

  • test.csv 测试集：检测模型创建后的准确率

  • train.csv 训练集：用于训练生成模型

导库 & 加载

import pandas as pd #数据分析库
import numpy as np #科学计算库
from pandas import Series, DataFrame

data_train = pd.read_csv("train.csv")
data_train.columns

有上，打印出训练集中的各特征字段名称

Data Dictionary

PassengerId  ==＞ 乘客ID
Survived ==＞ 乘客是否幸存 0=罹难，1=幸存
Pclass ==＞ 票类 1=一等舱，2=二等舱，3=三等舱
Name  ==＞ 乘客姓名
Sex  ==＞ 乘客性别
Age  ==＞ 乘客年龄
SibSp  ==＞ 兄弟姐妹/配偶数量
Parch  ==＞ 双亲/子女数量
Ticket  ==＞ 票号信息
Fare  ==＞ 船运票价
Cabin  ==＞ 客舱号
Embarked  ==＞ 出发港口

罗列出字典内字段之后，我们需要通过理性思维来筛选出影响乘客幸存的因素再加上船长的『Lady and kid first！』，甚至我们筛选条件可以再宽松一点，老人是否也可以提前乘上救生艇，这个后面再定，所以稍加思考可知

影响因素（暂定）包括：Sex、Pclass、Age

Exploratory Data Analysis

1、处理数据

data_train.info()

打印得到：

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId    891 non-null int64
Survived       891 non-null int64
Pclass         891 non-null int64
Name           891 non-null object
Sex            891 non-null object
Age            714 non-null float64
SibSp          891 non-null int64
Parch          891 non-null int64
Ticket         891 non-null object
Fare           891 non-null float64
Cabin          204 non-null object
Embarked       889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.6+ KB

可知：数据集包含891条数据，其中年龄Age有177条缺失，客舱号及出发港口均有不同程度的记录值缺失，这样看还不是很明确，换一下api查看，关于Pandas的DataFrame相关函数，可以参考另一篇文章传送门

data_train.describe()

打印如下

PassengerId Survived Pclass Age SibSp Parch Fare
count 891.000000 891.000000 891.000000 714.000000 891.000000 891.000000 891.000000
mean 446.000000 0.383838 2.308642 29.699118 0.523008 0.381594 32.204208
std 257.353842 0.486592 0.836071 14.526497 1.102743 0.806057 49.693429
min 1.000000 0.000000 1.000000 0.420000 0.000000 0.000000 0.000000
25% 223.500000 0.000000 2.000000 NaN 0.000000 0.000000 7.910400
50% 446.000000 0.000000 3.000000 NaN 0.000000 0.000000 14.454200
75% 668.500000 1.000000 3.000000 NaN 1.000000 0.000000 31.000000
max 891.000000 1.000000 3.000000 80.000000 8.000000 6.000000 512.329200

以上表格才稍微能看：
mean（平均数）得知Survived（存活）率约为38%；
Pclass=一等舱数＜Pclass=二/三等舱数；
乘客平均年龄为29岁，最大是80岁
等等…

2、特征工程

接着我们用点手段看最直观的图，使用绘图库Matplotlib

import matplotlib.pyplot as plt

figure = plt.figure() #调用Figure对象
figure.set(alpha = 1) #设置色值透明度

plt.subplot2grid((3,5),(0,0),colspan=1) #使用子图
data_train.Survived.value_counts().plot(kind='bar') #绘制柱状图
plt.title(u"获救情况『1为幸存』")
plt.ylabel(u"人数")

plt.subplot2grid((3,5),(0,2),colspan=1)
data_train.Pclass.value_counts().plot(kind='bar')
plt.title(u"程票类型")
plt.ylabel(u"人数")

plt.subplot2grid((3,5),(0,4),colspan=1)
plt.scatter(data_train.Survived, data_train.Age) #绘制散点图
plt.grid(b=True, which='major', axis='y') #网格线绘制
plt.title(u"各年龄层幸存情况『1为幸存』")
plt.ylabel(u"年龄")

plt.subplot2grid((3,5),(2,0),colspan=2)
data_train.Age[data_train.Pclass==1].plot(kind='kde') #绘制曲线图
data_train.Age[data_train.Pclass==2].plot(kind='kde')
data_train.Age[data_train.Pclass==3].plot(kind='kde')
plt.legend((u"一等舱", u"二等舱", u"三等舱"), loc='best')
plt.title(u"各舱乘客年龄分布")
plt.xlabel(u"年龄")
plt.ylabel(u"占比")

plt.subplot2grid((3,5),(2,4))
data_train.Embarked.value_counts().plot(kind='bar')
plt.title(u"各出港口登船情况")
plt.ylabel(u"人数")
plt.show()

运行得到绘图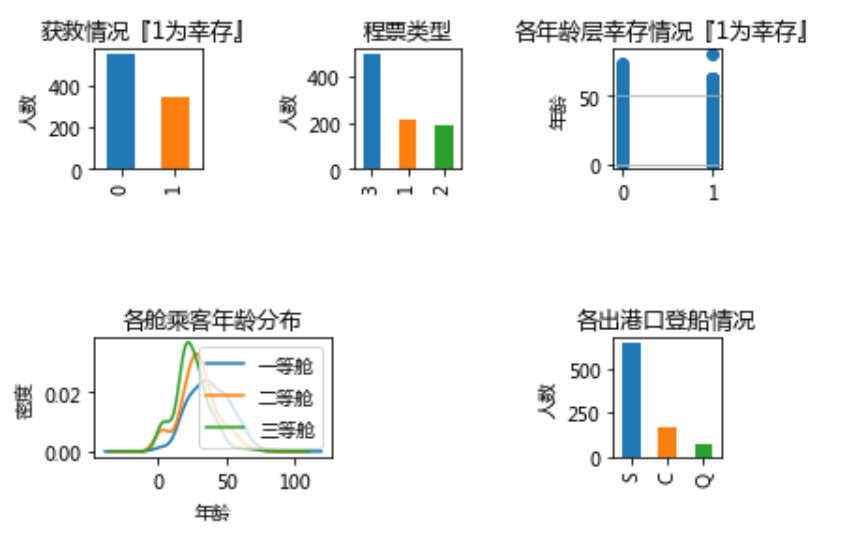

注：以上是合成一张大网格罗列出的绘图，代码运行观看每一张更为直观
从上图种种可看出：

  • 大致有300多人获救

  • 有一半以上购买三等舱

  • 各年龄层获救/罹难均有，分布较广

  • 三等舱和二等舱总体趋势相似，并且年龄层占比最多的是在20、30岁左右，一等舱最多是40岁左右乘客

  • 出港口人数以S（英国南安普敦（Southampton））最多，其次是C（法国 瑟堡-奥克特维尔（Cherbourg-Octeville）），最后是Q（爱尔兰 昆士敦（Queenstown）），不难理解，人数越多越有可能是出发港口，其他均是途径。

现在我们有一些疑问了：

① 这三百多人获救与购买不同等级舱有无关系？
② 年龄和性别对获救的影响大吗？（毕竟船长发过话）
③ 出港口的不同是不是也会影响乘客获救？

下面验证上面三个问题

Survived_No = data_train.Pclass[data_train.Survived == 0].value_counts()
Survived_Yes = data_train.Pclass[data_train.Survived == 1].value_counts()
df = pd.DataFrame({u"获救": Survived_Yes, u"未获救": Survived_No})
df.plot(kind='bar', stacked=True)
plt.title(u"各等级舱获救情况")
plt.xlabel(u"舱级")
plt.ylabel(u"人数")
plt.show

运行得到绘图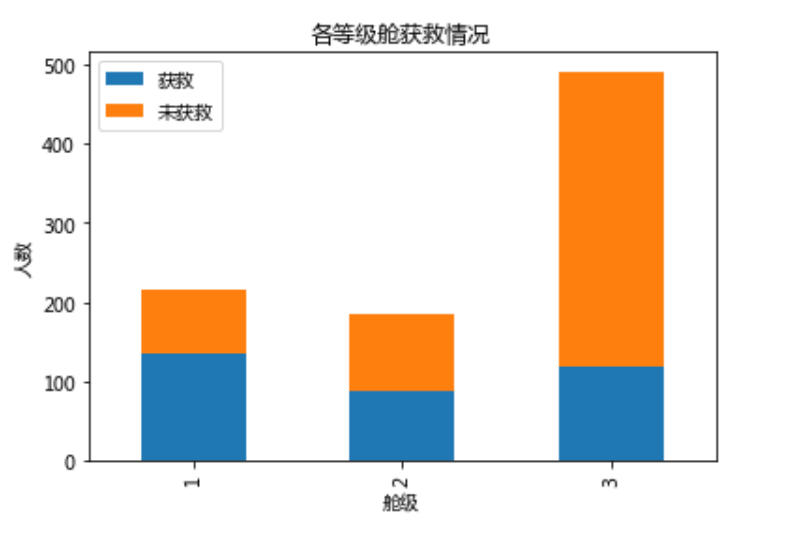

你看可以很明显的看出舱级越高幸存概率越大，这是决定因素之一

在看第二个问题

Survived_m = data_train.Survived[data_train.Sex == 'male'].value_counts()
Survived_f = data_train.Survived[data_train.Sex == 'female'].value_counts()
df = pd.DataFrame({u"男性": Survived_m, u"女性": Survived_f})
df.plot(kind='bar', stacked=True)
plt.title(u"各性别获救情况")
plt.xlabel(u"性别")
plt.ylabel(u"人数")
plt.show

运行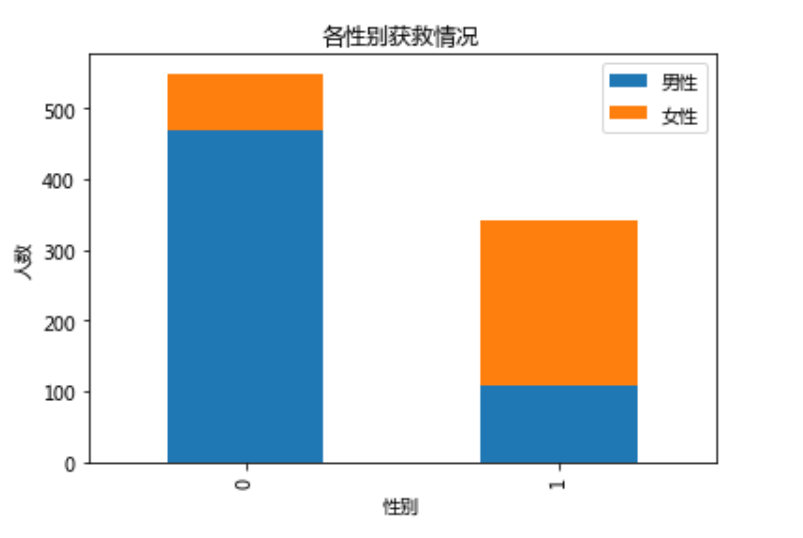

果然女性乘客获救比例比男性大很多，性别无疑也是作为模型中的重要的特征之一
同样年龄（取分割线为30岁，平均岁数）也可以尝试一下，并没有发现什么，但是随着分割的岁数越来越大，可以发现遇难的概率也是越来越大的，这也很符合常识，年迈的虽然会优先对待，但在那种恶劣处境下，毕竟求生本领还是很弱的。

看最后一个问题

Survived_No = data_train.Embarked[data_train.Survived == 0].value_counts()
Survived_Yes = data_train.Embarked[data_train.Survived == 1].value_counts()
df = pd.DataFrame({u"获救": Survived_Yes, u"未获救": Survived_No})
df.plot(kind='bar', stacked=True)
plt.title(u"各出港口乘客获救情况")
plt.xlabel(u"出港口")
plt.ylabel(u"人数")
plt.show

运行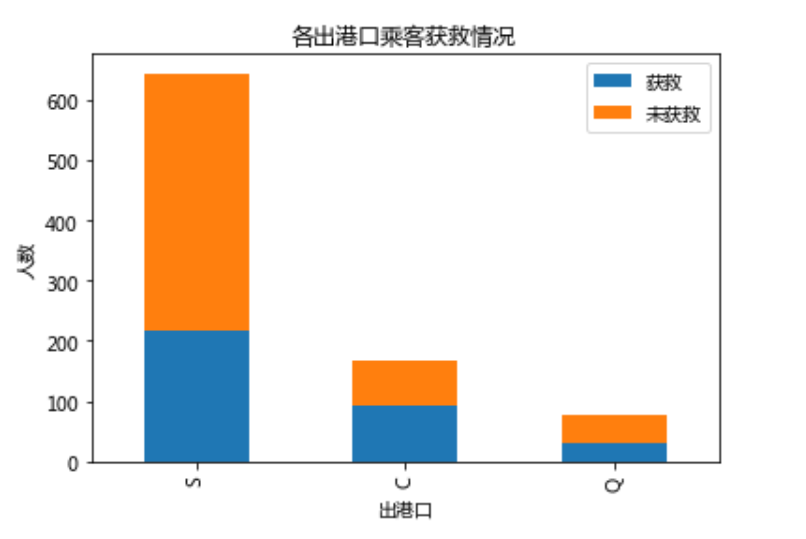

不怎么看的出来， 如果要解释从出发港口出发的乘客获救的几率大一点似乎也没多大说服力。暂时不管

既然这样，那条件继续细分

fig = plt.figure()
plt.title("各等级舱男女获救情况")

plot1 = fig.add_subplot(141) #表示1*4网格 第一子图
data_train.Survived[data_train.Sex=='male'][data_train.Pclass !=3].value_counts().plot(kind='bar', label="male highlevel", color='#FEB838')
plot1.set_xticklabels([u"获救", u"未获救"], rotation = 0)
plot1.legend([u"男性/高等舱"], loc='best')

plot2 = fig.add_subplot(142, sharey = plot1) 
data_train.Survived[data_train.Sex=='male'][data_train.Pclass ==3].value_counts().plot(kind='bar', label="male lowlevel", color='#fcce0b')
plot2.set_xticklabels([u"获救", u"未获救"], rotation = 0)
plot2.legend([u"男性/低等舱"], loc='best')

plot3 = fig.add_subplot(143, sharey = plot1) 
data_train.Survived[data_train.Sex=='female'][data_train.Pclass !=3].value_counts().plot(kind='bar', label="male lowlevel", color='#BA6564')
plot3.set_xticklabels([u"获救", u"未获救"], rotation = 0)
plot3.legend([u"女性/高等舱"], loc='best')

plot4 = fig.add_subplot(144, sharey = plot1) 
data_train.Survived[data_train.Sex=='female'][data_train.Pclass ==3].value_counts().plot(kind='bar', label="male lowlevel", color='#ff6d6d')
plot4.set_xticklabels([u"获救", u"未获救"], rotation = 0)
plot4.legend([u"女性/低等舱"], loc='best')

plt.show()

运行如下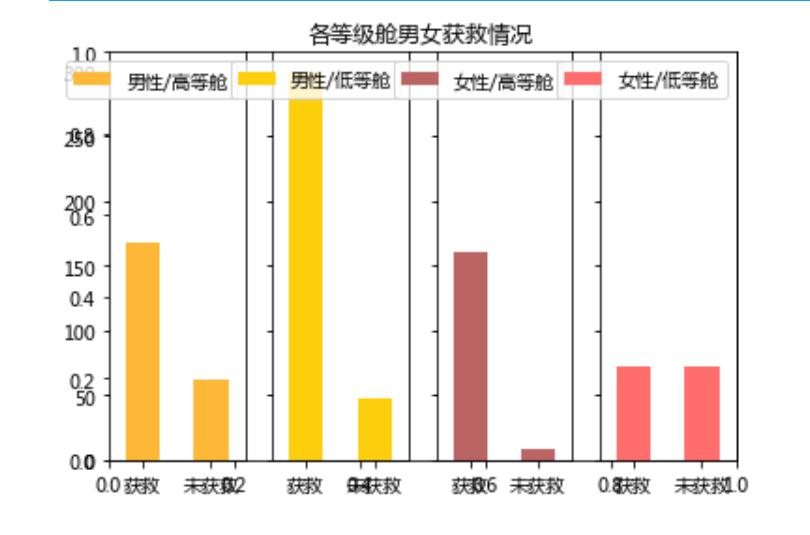

继续

f = data_train.groupby(['SibSp', 'Survived'])
df = pd.DataFrame(f['PassengerId'].count())
df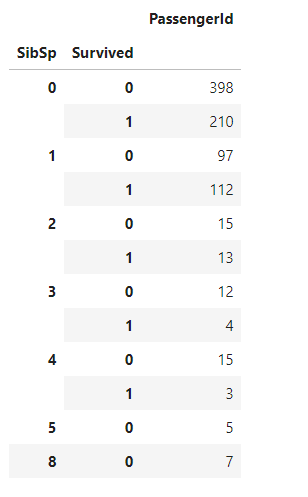

f = data_train.groupby(['Parch', 'Survived'])
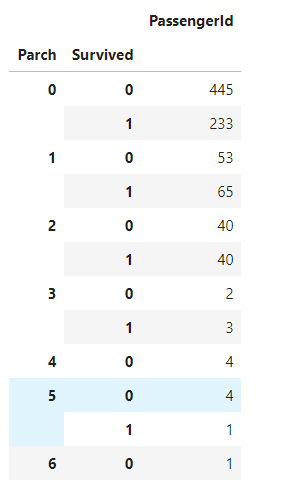
df = pd.DataFrame(f['PassengerId'].count())
df

还是看不出必然关系，那就先清洗一下数据，对缺失值做些处理，先从Cabin、Age缺失最严重却又是重要特征入手

3、缺失数据处理（清理数据）

通常遇到缺失值，最常见的处理方式有这些

  • 1.如果缺失的样本字段值占比很多，一般都需要舍去，以防形成噪声影响结果

  • 2.如果缺失样本占比适中，并且该属性是非连续性的特征属性，即分类属性的话，可引入NaN作为新类别特征

  • 3.如果缺失样本占比适中，并且该属性是连续性的特征属性，可以考虑步长step，并将其离散化分布

  • 4.如果缺失样本占比极少，可考虑手动加入拟合数据

可以尝试随机森林，一种集成学习模型，训练多个决策树，考虑多个结果做预测，这里使用sklearn库中的随机森林：

它的随机性体现在

  • 从原来的训练数据集随机（带放回样本）取一个子级作为森林中某个决策树的训练数据集

  • 每一次选择分叉的特征时，限定为在随机选择的特征的子级中寻找一个特征

它的优势体现在

  • 消除决策树容易过拟合的缺点

  • 减小预测的方差：预测值不会因为训练数据小变化而发生剧烈变化

这里用scikit-learn 的Random-forest拟合缺失的年龄数据

拟合缺失数据

from sklearn.ensemble import RandomForestRegressor

data_train = pd.read_csv("train.csv")
def fill_missing_age(df):
    # 新建一个随机森林回归对象，并把已确定的特征值存入
    df_age = df[['Age','Fare','Parch','SibSp','Pclass']]
    
    # 分成年龄缺失和不缺失两部分
    age_known = df_age[df_age.Age.notnull()].values
    age_unknown = df_age[df_age.Age.isnull()].values
    
    y = age_known[:, 0] #已知年龄区的所有年龄值
    X = age_known[:, 1:] #已知年龄区的所有特征属性值

    # 解释构造函数各参数
    # random_state：此参数让结果容易复现。特定的随机状态值将会产生相同的结果。
    # n_estimators：想建立的子树数量（前提是在利用最大投票数或平均值预测之前）
    # n_jobs：告诉引擎可以有多少处理器可以使用（-1代表无限制，1代表只能使用一个处理器）
    rfr= RandomForestRegressor(random_state=0, n_estimators=2000, n_jobs=-1)
    rfr.fit(X, y) # 训练到回归模型中
    
    # 进行结果预测
    predict_age=rfr.predict(age_unknown[:, 1::])
    # 预测值填充缺失数据
    df.loc[(df.Age.isnull()),'Age'] = predict_age
    
    return df, rfr

def fill_Cabin_type(df):
    df.loc[(df.Cabin.notnull()), 'Cabin'] = "Yes"
    df.loc[(df.Cabin.isnull()), 'Cabin'] = "No"
    return df

data_train, rfr = fill_missing_age(data_train)
data_train = fill_Cabin_type(data_train)
data_train

运行得到如下（只截取部分）

独热编码

dummies_Sex = pd.get_dummies(data_train['Sex'], prefix='Sex')
dummies_Cabin = pd.get_dummies(data_train['Cabin'], prefix='Cabin')
dummies_Pclass = pd.get_dummies(data_train['Pclass'], prefix='Pclass')
dummies_Embarked = pd.get_dummies(data_train['Embarked'], prefix='Embarked')

df = pd.concat([data_train, dummies_Sex, dummies_Cabin, dummies_Pclass, dummies_Embarked], axis=1)
df.drop(['Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'], axis=1, inplace=True)
df

得到

对幅度过大特征属性值进行归一化 加速逻辑回归收敛

import sklearn.preprocessing as preprocessing
scaler = preprocessing.StandardScaler()

age_scale = scaler.fit(df['Age'].values.reshape(-1,1))
df['Age_scaled'] = scaler.fit_transform(df['Age'].values.reshape(-1,1), age_scale)
fare_scale = scaler.fit(df['Fare'].values.reshape(-1,1))
df['Fare_scaled'] = scaler.fit_transform(df['Fare'].values.reshape(-1,1), fare_scale)
df

得到

4、建模

取出特征字段 模型建模

from sklearn import linear_model

train_df = df.filter(regex='Survived|Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
train_np = train_df.values

y = train_np[:, 0]
X = train_np[:, 1:]

# 逻辑回归构造参数解析
# C：正则化系数λ的倒数，通常默认为1
# penalty：正则化选择惩罚项参数 可选择“l1”和“l2”正则，默认“l2” 主要为解决过拟合问题
# penalty参数的选择会影响我们损失函数优化算法的选择。即参数solver的选择，
# 如果是L2正则化，那么4种可选的算法{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’}都可以选择。
# 但是如果penalty是L1正则化的话，就只能选择‘liblinear’了。
# 这是因为L1正则化的损失函数不是连续可导的，
# 而{‘newton-cg’, ‘lbfgs’,‘sag’}这三种优化算法时都需要损失函数的一阶或者二阶连续导数。而‘liblinear’并没有这个依赖。
lr_clf = linear_model.LogisticRegression(C=1.0, penalty='l1', solver='liblinear', tol=1e-6)
lr_clf.fit(X, y)

lr_clf

最简版baseline

data_test = pd.read_csv("test.csv")
data_test.loc[ (data_test.Fare.isnull()), 'Fare' ] = 0

# 接着我们对test_data做和train_data中一致的特征变换
# 首先用同样的RandomForestRegressor模型填上丢失的年龄
tmp_df = data_test[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]
null_age = tmp_df[data_test.Age.isnull()].values

# 根据特征属性X预测年龄并补上
X = null_age[:, 1:]
predictedAges = rfr.predict(X)
data_test.loc[ (data_test.Age.isnull()), 'Age' ] = predictedAges

data_test = set_Cabin_type(data_test)
dummies_Cabin = pd.get_dummies(data_test['Cabin'], prefix= 'Cabin')
dummies_Embarked = pd.get_dummies(data_test['Embarked'], prefix= 'Embarked')
dummies_Sex = pd.get_dummies(data_test['Sex'], prefix= 'Sex')
dummies_Pclass = pd.get_dummies(data_test['Pclass'], prefix= 'Pclass')


df_test = pd.concat([data_test, dummies_Cabin, dummies_Embarked, dummies_Sex, dummies_Pclass], axis=1)
df_test.drop(['Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'], axis=1, inplace=True)
df_test['Age_scaled'] = scaler.fit_transform(df_test['Age'].values.reshape(-1,1), age_scale_param)
df_test['Fare_scaled'] = scaler.fit_transform(df_test['Fare'].values.reshape(-1,1), fare_scale_param)
df_test

预测上传查询得分

test = df_test.filter(regex='Age_.*|SibSp|Parch|Fare_.*|Cabin_.*|Embarked_.*|Sex_.*|Pclass_.*')
predictions = clf.predict(test)
result = pd.DataFrame({'PassengerId':data_test['PassengerId'].values, 'Survived':predictions.astype(np.int32)})
result.to_csv("logistic_regression_predictions.csv", index=False)

总结

初始得分0.7655，先结篇后面还需做很多优化处理，朝满分前进！

文章作者: Leo·Cheung
文章链接: http://tufusi.com/2019/11/25/%E3%80%90%E7%AB%9E%E8%B5%9B%E4%B8%93%E9%A2%98%E3%80%91Kaggle%20Titanic%E5%85%A5%E9%97%A8/
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 ONE·PIECE！
数据竞赛 算法 Kaggle
打赏
  • 微信
  • 支付宝
评论
简